Линия пересечения плоскостей онлайн. Пересечение плоскостей Что такое прямая пересечения плоскостей
В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.
По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.
Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.
Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = (A 1 , B 1 , C 1) и n 2 → = (A 2 , B 2 , C 2) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:
n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R
Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.
Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .
Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.
Пример 1
Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .
Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .
Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.
Рассмотрим решение примера
Пример 2
Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x - 2 y + z - 3 = 0 . Определите, принадлежат ли точки M 0 (1 , - 1 , 0) и N 0 (0 , - 1 3 , 1) прямой линии пересечения плоскостей.
Решение
Начнем с точки М 0 . Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · (- 1) + 1 = 0 1 - 2 · (- 1) + 0 - 3 = 0 ⇔ 0 = 0 0 = 0 .
В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.
Подставим в оба уравнения плоскости координаты точки N 0 (0 , - 1 3 , 1) . Получаем 2 · 0 + 3 · - 1 3 + 1 = 0 0 - 2 · - 1 3 + 1 - 3 = 0 ⇔ 0 = 0 - 1 1 3 = 0 .
Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.
Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.
Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.
Приведем пример.
Пример 3
Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.
Решение
Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 .
Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.
Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:
x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 ⇔ x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z
Введем произвольное действительное число λ и примем, что z = λ .
Тогда x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z ⇔ x + 0 y = - 7 - 3 λ 2 x + 3 y = - 2 - 3 λ .
Для решения полученной системы уравнений применим метод Крамера:
∆ = 1 0 2 3 = 1 · 3 - 0 · 1 = 2 ∆ x = - 7 - 3 λ 0 - - 3 λ 3 = - 7 - 3 λ · 3 - 0 · (- 2 - 3 λ) = 21 - 9 λ ⇒ x = ∆ x ∆ = - 7 - 3 λ ∆ y = 1 - 7 - 3 λ 2 - 2 - 3 λ = 1 · - 2 - 3 λ - - 7 - 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = - 7 - 3 λ y = 4 + λ z = λ , где λ ∈ R .
Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = - 7 - 3 · 0 y = 4 + 0 z = 0 ⇔ x = - 7 y = 4 z = 0 .
Это позволяет нам получить координаты искомой точки - 7 , 4 , 0 .
Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей - 7 + 3 · 0 + 7 = 0 2 · (- 7) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .
Ответ : - 7 , 4 , 0
Направляющий вектор прямой, по которой пересекаются две плоскости
Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.
Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.
Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = (A 1 , B 1 , C 1) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = (A 2 , B 2 , C 2) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .
Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = (A 1 , B 1 , C 1) и n 2 → = A 2 , B 2 , C 2 .
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ - это параметр, который может принимать любые действительные значения, отличные от нуля.
Пример 4
Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y - 3 z - 2 = 0 x - z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.
Решение
Плоскости x + 2 y - 3 z - 2 = 0 и x - z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , - 3 и n 2 → = 1 , 0 , - 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:
a → = n → 1 × n 2 → = i → j → k → 1 2 - 3 1 0 - 1 = i → · 2 · (- 1) + j → · (- 3) · 1 + k → · 1 · 0 - - k → · 2 · 1 - j → · 1 · (- 1) - i → · (- 3) · 0 = - 2 · i → - 2 j → - 2 k →
Запишем ответ в координатной форме a → = - 2 , - 2 , - 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».
Ответ: a → = - 2 , - 2 , - 2
Переход к параметрическим и каноническим уравнениям прямой в пространстве
Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z - координаты направляющего вектора прямой, x 1 , y 1 , z 1 - координаты некоторой точки прямой, а λ - параметр, принимающий произвольные действительные значения.
От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.
Рассмотрим написанное выше на примере.
Пример 5
Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.
Решение
Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , - 1 плоскости 2 x + y - z - 1 = 0 и n 2 → = (1 , 3 , - 2) плоскости x + 3 y - 2 z = 0:
a → = n 1 → × n 2 → = i → j → k → 2 1 - 1 1 3 - 2 = i → · 1 · (- 2) + j → · (- 1) · 1 + k → · 2 · 3 - - k → · 1 · 1 - j → · 2 · (- 2) - i → · (- 1) · 3 = i → + 3 · j → + 5 · k →
Координаты направляющего вектора прямой a → = (1 , 2 , 5) .
Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ 2 x + y - z = 1 x + 3 y - 2 z = 0 .
Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 - 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ:
2 x + y - z = 1 x + 3 y - 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R
Применяем для решения полученной системы уравнений метод Крамера:
∆ = 2 1 1 3 = 2 · 3 - 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = (1 + λ) · 3 - 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ - (1 + λ) · 1 = - 1 + 3 λ ⇒ y = ∆ y ∆ = - 1 + 3 λ 5 = - 1 5 + 3 5 · λ
Получаем: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 y = - 1 5 + 3 5 z = λ
Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = - 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ x - 1 1 = y - 1 3 = z - 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Ответ: x - 1 1 = y - 1 3 = z - 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Данная задача имеет еще один способ решения.
Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .
Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y λ = z - z 1 a z ⇔ x - x 1 a x = y - y 1 a y = z - z 1 a z
Применим данный способ к решению задачи.
Пример 6
Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.
Решение
Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ .
Это параметрические уравнения прямой в пространстве.
Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ ⇔ λ = x - 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x - 3 5 1 5 = y + 1 5 3 5 = z 1
Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.
Ответ: x - 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Задача на пересечение плоскостей в силу своей важности носит у ряда авторов наименование «позиционная задача № 2».
Из стереометрии известно, что линией пересечения двух плоскостей служит прямая. В предыдущих предварительных задачах, где речь шла о частных случаях пересечения плоскостей, мы исходили из этого определения.
Как известно, чтобы построить ту или иную прямую, в простейшем случае требуется отыскать две точки, принадлежащие этой прямой. В случае задания плоскости следами в качестве этих двух точек выступают точки пересечения одноименных следов пересекающихся плоскостей.
Примеры для самостоятельной работы
Упражнение 5.1
Построить линии пересечения плоскостей, заданных следами (рис. 72):
- а) горизонтально проецирующей I и фронтально проецирующей А;
- б) горизонтально проецирующей Z и плоскости общего положения Q;
- в) двух плоскостей общего положения I и 0.
Рис. 72
На рис. 73 приведены ответы к этому упражнению.
Для случаев задания плоскостей локальными плоскими фигурами уместно использование по крайней мере двух различных путей решения.

Рис. 73
Первый путь решения - использование трехступенного алгоритма нахождения точки встречи прямой общего положения с плоскостью общего положения. Для нахождения линии пересечения двух треугольников один из треугольников оставляют без изменения, а второй мысленно расчленяют на отдельные отрезки, представляя их в качестве прямых общего положения. Сначала находят точку пересечения одной из прямых общего положения с плоскостью треугольника. Затем находят еще одну недостающую точку, принадлежащую искомой линии. Это делается аналогичным путем, повторяя всю описанную последовательность действий.
Упражнение 5.2
По заданным координатам вершин двух треугольников ЛВС и DEK построить эпюр последних и найти линию их пересечения. Указать видимость элементов обоих треугольников на эпюре: А (0, 9, 2); ?(10, 1, 16); С (23, 14, 9); D (3, 17, 18); ?(22, 11, 17); ?(12,0, 2). Для нахождения линий пересечения треугольников рекомендуется сначала найти точку встречи прямой KD с треугольником АВС, а затем точку встречи прямой СВ с треугольником EDK.
Общий вид полученного эпюра приведен на рис. 74.
Второй путь решения - использование двух вспомогательных секущих плоскостей уровня.
Заданные пересекающиеся плоские фигуры следует дважды пересечь вспомогательными плоскостями уровня (одноименными либо разноименными - безразлично), например двумя горизонтальными плоскостями уровня.
Нетрудно понять, что одноразовое рассечение позволяет отыскать две пересекающиеся прямые h l и И 2 , дающие одну точку А, принадлежащую искомой линии пересечения (рис. 75). Проводя еще одну аналогичную вспомогательную плоскость на некотором расстоянии

Рис. 74

Рис. 75
от первой, получают аналогичное построение и еще одну точку. Соединяя одноименные проекции двух полученных точек, находят искомую линию пересечения двух плоскостей.
Упражнение 5.3

По заданным координатам точек двух треугольных фигур построить эпюр последних, на котором построить с использованием вспомогательных плоскостей линию пересечения треугольников. Указать видимость элементов обоих треугольников на эпюре:
к АВС. А (16, 5, 17); Я (10, 19,
A DEF: D (24, 12, 14); ? (4, 18,
Общий вид решенной задачи изображен на рис. 76.
Упражнение 5.4
Для закрепления навыков нахождения линии пересечения двух плоскостей приводится задача, решение которой дается в динамике построений в соответствии со ступенями алгоритма.
Найти линию пересечения двух плоскостей общего положе- р ис jq
ния, заданных двумя треугольниками АВС и DEF, и определить видимость их взаимопроникновения (рис. 77).
Решение примера сводится к отысканию точек пересечения сторонами (прямыми) ААВС с плоскостью общего положения, заданной ADEF. Алгоритм решения этого примера известен.
Заключаем сторону (прямую) АС ЬЛВС во вспомогательную фронтально проецирующую плоскость т _1_ П 2 (рис. 78).
Фронтальный след этой вспомогательной плоскости пересекает проекции сторон D 2 E 2 глЕ 2 - 1 2 и D 2 F 2 пт 2 = 2 2 в точках 1 2 и 2 2 . Проекционные линии связи позволяют на горизонтальной плоскости проекций определить линию пересечения (1 !~2 2) = n AD X E X F { . Тогда точка К 1 и ее проекция К 2 определяют точку пересечения прямой АС с ADEF.
Повторяем алгоритм нахождения точки пересечения стороны ААВС прямой ВС с ADEF. Заключаем ВС во вспомогательную фронтально проецирующую плоскость р _L П 2 (рис. 79).


Находим проекции точек 3 и 4 и на горизонтальной плоскости проекций определяем проекцию точки пересечения прямой В 1 С [
с линией пересечения (3,-4,):
![]()
Проекционная линия связи позволяет найти ее фронтальную проекцию точку М 2 .
Соединяем найденные точки Ки Ми находим линию пересечения двух плоскостей общего положения AABC n ADEF= АЖ (рис. 80).
Видимость сторон ААВС относительно ADEF определяется с помощью конкурирующих точек. Сначала определяем видимость геометрических фигур на плоскости проекций П 2 . Для этого через конкурирующие точки 5 и 6 (5 2 = 6 2) проводим проекционную линию связи, перпендикулярную оси проекций х п (рис. 81).
По горизонтальным проекциям 5 У и 6 { точек 5 и 6, в которых линия проекционной связи соответственно пересекает скрещивающиеся прямые АС 4 DF, выясняется, что точка 6 более удалена от плоскости проекций П 2 , чем точка 5. Поэтому точка 6 и прямая DF, которой она принадлежит, видимы относительно плоскости проекций П 2 . Отсюда следует, что отрезок (К 2 -6 2) будет невидимым. Аналогично определяем видимость сторон АЛВС и ADEF - ВС и DF, т.е. отрезок (Ж 2 -8 2) будет невидимым.
Видимость ААВС и ADEF относительно плоскости проекций П j, устанавливается аналогично. Для определения видимости скрещивающихся прямых АС * DF и ВС ±DF относительно плоскости проекций П] через конкурирующие точки 9 1 = 10 1 и11 1 = 12 1 проводим проекционные линии связи перпендикулярно х п. По фронтальным проекциям этих конкурирующих точек устанавливаем, что проекции точек 10 2 и 12 2 более удалены от плоскости проекций П { . Следовательно, отрезки (А^-ЮД и (М г 2 1) будут невидимыми. Отсюда видимость ААВС и ADEF наглядно представлена на рис. 82.




УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом
между двумя плоскостями будем понимать один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1
и α 2 равен одному из указанных смежных двугранных углов или ![]() . Поэтому
. Поэтому  . Т.к.
. Т.к.![]() и
и ![]() , то
, то
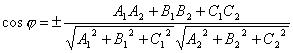 .
.
Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.
![]()
Условие параллельности двух плоскостей.
Две плоскости α 1 и α 2
параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит ![]() .
.
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
![]() или
или
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .
Таким образом, .
Примеры.
ПРЯМАЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
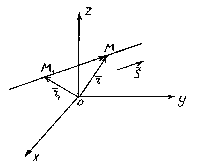
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .
Рассмотрим произвольную точку М(x,y,z)
на прямой. Из рисунка видно, что ![]() .
.
Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.
Запишем это уравнение в координатной форме.
Заметим, что ,
![]() и отсюда
и отсюда
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
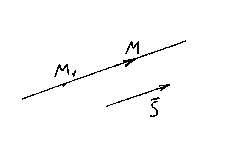
Пусть М
1 (x
1 , y
1 , z
1) – точка,
лежащая на прямой l
, и ![]() –
её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z)
и рассмотрим вектор .
–
её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z)
и рассмотрим вектор .
Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,
![]() – канонические
уравнения прямой.
– канонические
уравнения прямой.
Замечание 1.
Заметим, что канонические
уравнения прямой можно было получить из параметрических,исключив параметр t
. Действительно, из параметрических уравнений получаем ![]() или
или ![]() .
.
Пример.
Записать уравнение прямой ![]() в параметрическом виде.
в параметрическом виде.
Обозначим ![]() ,
отсюда x
= 2 + 3t
, y
= –1 + 2t
, z
= 1 –t
.
,
отсюда x
= 2 + 3t
, y
= –1 + 2t
, z
= 1 –t
.
Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид
Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально
записывать канонические уравнения прямой в виде![]() .
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает, что прямая
перпендикулярна соответствующей координатной оси.
.
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает, что прямая
перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям ![]() соответствует прямая перпендикулярная осям Ox
и Oy
или параллельная оси Oz
.
соответствует прямая перпендикулярная осям Ox
и Oy
или параллельная оси Oz
.
Примеры.
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
Построить прямую, заданную уравнениями ![]()

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:
Решив эту систему, найдем точку M 1 (1;2;0).
Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :
![]()

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.
Координаты точки
М
1
получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания
направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к
обоим нормальным векторам ![]() и
и ![]() .
Поэтому за направляющий вектор прямой l
можно взять векторное произведение нормальных векторов:
.
Поэтому за направляющий вектор прямой l
можно взять векторное произведение нормальных векторов:
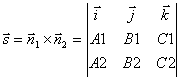 .
.
Пример.
Привести общие уравнения прямой
![]() к каноническому виду.
к каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:
![]()
Нормальные векторы
плоскостей, определяющих прямую имеют координаты ![]() Поэтому направляющий вектор
прямой будет
Поэтому направляющий вектор
прямой будет
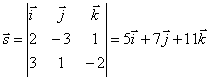 .
Следовательно, l
:
.
Следовательно, l
: ![]() .
.
УГОЛ МЕЖДУ ПРЯМЫМИ
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой
Билет 6 Записать выражение для угла между прямой и плоскостью, условие параллельности и перпендикулярности прямой и плоскости.
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямами плоскость заданы уравнениями
 Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда
Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда ![]() .
.
Если угол между векторами и тупой, то он равен . Следовательно ![]() . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим
. Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим  .
.
Условие перпендикулярности прямой и плоскости.
Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. ![]() .
.
Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.
Билет 7 . Дать определение эллипса. Записать уравнение эллипса в канонической форме. Вершины, фокусы, оси и эксцентриситет эллипса.
Определение: Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.
Пусть F 1 и F 2 – фокусы эллипса. Начало O системы координат расположим на середине отрезка F 1 F 2 . Ось Ox направим вдоль этого отрезка, ось Oy – перпендикулярно к этому отрезку (рис.).

Определение: Точки пересечения эллипса с его осями симметрии называются вершинами эллипс а, центр симметрии – центром эллипса , отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса , половина его длины – большой полуосью эллипса . Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса , половина его длины – малой полуосью. Величина называется эксцентриситетом эллипса .
Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (–a ;0), (a ;0),(0; –b ), (0;b ), большая полуось равна a , малая полуось равна b . Величина c , являющаяся половиной расстояния между фокусами, определяется из формулы c 2 = a 2 – b 2 .
Эксцентриситет эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0< <1.
Уравнение называется каноническим уравнением эллипса .

Билет 8 Дать определение гиперболы. Записать уравнение гиперболы в канонической форме. Вершины, фокусы, оси, асимптоты и эксцентриситет гиперболы,
Определение: Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось Ox направим вдоль этого отрезка, а ось ординат – перпендикулярно к нему.
Уравнение называется каноническим уравнением гиперболы.
Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси Ox и Oy , а начало координат – центр симметрии гиперболы.
Определение: Точки пересечения гиперболы, заданной каноническим уравнением с осью Ox называются вершинами гиперболы , отрезок между ними называется действительной осью гиперболы . Отрезок оси ординат между точками (0;–b ) и (0;b ) называется мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина называется эксцентриситетом гиперболы.
Замечание: Из равенства b 2 = c 2 – a 2 следует, что c >a , то есть у гиперболы >1. Эксцентриситет характеризует угол между асимптотами, чем ближе к 1, тем меньше этот угол.

Билет 9. Дать определение параболы. Записать уравнение параболы в канонической форме. Директриса, фокус параболы
Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки F и заданной прямой d, не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы .
Директориальное свойство параболы Точка F называется фокусом параболы, прямая d - директрисой параболы, середина O перпендикуляра, опущенного из фокуса на директрису, - вершиной параболы, расстояние p от фокуса до директрисы - параметром параболы, а расстояние p2 от вершины параболы до её фокуса - фокусным расстоянием (рис,а). Прямая, перпендикулярная директрисе и проходящая через фокус, называется осью параболы (фокальной осью параболы). Отрезок FM , соединяющий произвольную точку M параболы с её фокусом, называется фокальным радиусом точки M. Отрезок, соединяющий две точки параболы, называется хордой параболы.
Для произвольной точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Сравнивая директориальные свойства эллипса, гиперболы и параболы, заключаем, что эксцентриситет параболы по определению равен единице
.Геометрическое определение параболы , выражающее её директориальное свойство, эквивалентно её аналитическому определению - линии, задаваемой каноническим уравнением параболы:

Билет 10 . Что такое квадратная, единичная, симметрическая, ортогональная матрица. Дать определение транспонированной и обратной матрицы.
Определение 1. Матрицей называется прямоугольная таблица из чисел, содержащая - строк и - столбцов. .
Определение 2. Числа И называются Порядками матрицы (или говорят, что матрица имеет размер )
Определение 3. Числа , входящие в состав данной матрицы, называются ее элементами .
1.Определение 4. Матрица называется Квадратной если число строк равно числу столбцов. В случае квадратной матрицы вводятся понятия Главной диагонали (это числа - ) и Побочной диагонали (это числа - ).
2.Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Более формально, симметричной называют такую матрицу , что .
Это означает, что она равна её транспонированной матрице:
3. Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице. Например, единичной матрицей третьего порядка является матрица

Ортогональная матрица
Квадратная матрица A , для которой A -1 = A T называется ортогональной матрицей . Основные свойства ортогональной матрицы: Модуль определителя ортогональной матрицы равен единице. Это свойство следует из свойств определителей:
Сумма квадратов элементов любого столбца ортогональной матрицы равна единице.
Скалярное произведение строки на саму себя равно 1, а на любую другую строку - 0. Так же и для столбцов.
Сумма произведений элементов любой строки ортогональной матрицы на соответствующие элементы другой строки равна нулю.
Обратной матрицей
называется матрица, которая при умножении как справа, так и слева на данную матрицу дает единичную матрицу.Обозначим обратную матрицу к матрице А
через , тогда согласно определению получим: ![]() где Е
– единичная матрица.
где Е
– единичная матрица.
Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является
det(A ) ≠ 0 или rank(A ) = N .
Свойства обратной матриц
· , где обозначает определитель.
· для любых двух обратимых матриц и .
· , где обозначает транспонированную матрицу.
· для любого коэффициента .
· Если необходимо решить систему линейных уравнений , (b - ненулевой вектор) где - искомый вектор, и если существует, то . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Транспонированная матрица - матрица , полученная из исходной матрицы заменой строк на столбцы.
Формально, транспонированная матрица для матрицы размеров - матрица размеров , определённая как .
Билет 11. Что такое эквивалентные матрицы. Перечислите элементарные преобразования матриц. Что можно сказать о рангах эквивалентных матриц.
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Элементарными преобразованиями над строками матриц называются следующие преобразования строк:
1. умножение строки на ненулевое число;
2. перестановка двух строк;
3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число.
4. Если от матрицы к матрице перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают .
5. Метод элементарных преобразований
6. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
Билет 12 , Что такое базисный минор. Сформулируйте теорему о базисном миноре.
Определение. Ранг матрицы А - максимальный порядок неравного нулю минора (минор - определитель квадратной матрицы ). Обозначается .
Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие БМ, называются базисными строками и столбцами.
Определение.
Система столбцов ![]() называется линейно зависимой числа , не все равные нулю и такие что:
называется линейно зависимой числа , не все равные нулю и такие что:
Теорема о Базисном миноре
Столбцы матрицы , входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы линейно выражается через остальные столбцы из базисного минора.
В матрице размеров минор -го порядка называется базисным, если он отличен от нуля, а все миноры -ro порядка равны нулю или их вообще не существует.
Следствие. Если все столбцы матрицы линейно выражаются через столбцов , которые образуютлинейно независимую систему, то ранг матрицы .
Билет 13 Что такое однородная и неоднородная система уравнений. Что называется решением системы уравнений. Поясните термины: совместная система уравнений, несовместная система уравнений. Какие системы уравнений называются эквивалентными?
Определение 1. Если все свободные члены равны нулю, то система называется однородной, и неоднородной - в противном случае.
Определение 2. Решением системы называется совокупность из n чисел с 1 , с 2 , …, с n , при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств.
Определение 3. Система называется совместной (несовместной), если она имеет хотя бы одно решение (не имеет решений).
Определение 4. Совместная система линейных алгебраических уравнений называется определённой (неопределённой), если она имеет единственное решение (множество решений).
Определение.
Две системы линейных уравнений называют равносильными (эквивалентными ), если они имеют одни и те же решения.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками системы.
Билет 14 Что такое фундаментальная система решений однородной системы уравнений. Что называется общим решением однородной системы уравнений.
Определение. Базис пространства решений системы линейных однородных уравнений называется её фундаментальной системой решений.
Теорема о структуре общего решения однородной системы уравнений:
Любое решение однородной системы линейных уравнений определяется формулой
где X 1 , X 2 , … , X n − r - фундаментальная система решений однородной системы линейных уравнений и C 1 , C 2 , … , C n − r - произвольные постоянные.
Свойства общего решения однородной системы уравнений :
1. При любых значениях C 1 , C 2 , … , C n − r X , определяемое формулой (3), является решением системы (1).
2. Каково бы ни было решение X 0 , существуют числа C 1 0 , … , C n − r 0 такие, что
Вывод:
Чтобы найти фундаментальную систему и общее решение однородной системы, нужно найти базис ядра соответствующего линейного оператора.
Билет 16 . Дать определение линейного пространства и сформулировать его свойства.
Множество L называется линейным или векторным пространством , если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + y из L , называемый суммой x и y , причём:
x + y = y + x − сложение коммутативно;
x + (y + z) = (x + y) + z − сложение ассоциативно;
x +0 = x − существует единственный нулевой элемент 0 (x +0 = x для любого x из L );
x + (− x )= 0 − для каждого элемента x из L существует единственный противоположный элемент −x (x + (−x) = 0 для любого x изL ) .
2. Каждой паре x и α, где α − число, а x элемент из L , отвечает элемент α·x , наываемый произведением α и x , причём:
α·(β· x ) = (α·β)· x − умножнение на число ассоциативно: ;
1· x = x − для любого элемента x из L .
3. Операции сложения и умножения на число связаны соотношениями:
α·(x + y ) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;
(α + β)· x = α·x + β· x − умножнение на вектор дистрибутивно относительно сложения чисел.
Билет 17 . Подпространство линейного пространства. Его свойства. Линейная оболочка.
Определение линейного подпространства
Непустое подмножество L линейного пространства V называется линейным подпространством пространства V, если
1) u+v∈L ∀u,v∈L (подпространство замкнуто по отношению к операции сложения);
2) λv∈L ∀v∈L и любого числа λ (подпространство замкнуто по отношению к операции умножения вектора на число).
Свойство 1 Всякое подпространство линейного пространства R есть линейное пространство.
Свойство 2 dim M ≤ dim Rn.
Свойство 3 (о пополнении базиса) . Если (ep)k - базис в подпространстве M линейного пространства Rn, причем k < n, то можно так выбрать элементы в Rn ek+1, ek+2, . . . , en, что (ep)n будет базисом в Rn.
О п р е д е л е н и е.Линейная оболочка - это набор векторов, которые задают линейное подпространство. Строго говоря, линейная оболочка - это множество всех линейных комбинаций данных векторов. Так же обозначим особенности:
Билет 18 . Дать определение евклидова пространства. Поясните операцию нормирование вектора.
Определение Пусть V - векторное пространство. Говорят, что в V задано скалярное произведение, если любым двум векторам x, y ∈ V поставлено в соответствие действительное число, называемое скалярным произведением этих векторов и обозначаемое через xy или (x, y), так, что выполнены следующие условия (здесь x, y, z - произвольные векторы из V, а
t - произвольное действительное число):
1) xy = yx (скалярное произведение коммутативно);
2) (tx)y = t(xy);
3) (x + y)z = xz + yz (скалярное произведение дистрибутивно относительно сложения);
4) xx >=0, причем xx = 0 тогда и только тогда, когда x = 0.
Векторное пространство, в котором задано скалярное произведение, называется евклидовым. Свойства 1)–4) называются аксиомами евклидова пространства.
Вектор называют нормированным или единичным
, если его длина равна единице. Нормировать произвольный ненулевой вектор - это поделить его на длину. Получится единичный вектор, сонаправленный исходному.
Скалярное произведение произвольного вектора на единичный даст точную длину проекции этого вектора на направление единичного. Чтобы получить не просто длину, а сам вектор-проекцию, надо умножить эту длину на наш единичный вектор:
Билет 19 Что такое ортонормированный базис. Поясните процесс ортогонализации Грама-Шмидта на примере двумерного базиса.
Ортонормированная система, состоящая из n векторов n -мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.
Если e 1 , e 2 , ..., e n - ортонормированный базис n -мерного евклидова пространства и
x = x 1 e 1 + x 2 e 2 + ... + x n e n - разложение вектора x по этому базису, то координаты x i вектора x в ортонормированном базисе вычисляются по формулам x i =(x, e i ), i = 1, 2, ..., n .
ГРАМА-ШМИДТА, Дана линейно независимая система векторов b 1 , b 2 , …, b l , a l+1 , …, a n l ≥ 1 (1)часть, которой ортогональна, обозначим b l+1 ортогональную составляющую вектора а l+1 относительно ортогональной системыb 1 , b 2 , …, b l . Тогда1. Система векторовb 1 , b 2 , …, b l , b l+1 , a l+2 , …, a n (2) эквивалентна (1).
2. Система векторов (2) линейно независима, а ее часть b 1 , b 2 , …, b l , b l+1 – ортогональна.Используя, понятие ортогональной составляющей, опишем процесс превращения линейно независимой системы а 1 , а 2 , …, а n в ортогональную системуb 1 , b 2 , …, b n ненулевых векторов, который называется ортогонализацией системы а 1 , а 2 , …, а n .Этот процесс состоит из n–шагов, n–число векторов в исходной системе а 1 , а 2 , …, а n .
1 шаг. Полагаем b 1 =а 1 и получаем системуb 1 , а 2 , …, а n
2 шаг. Заменим в системе (3) вектор а 2 ортогональной составляющей относительно b 1 , и получим систему:b 1 ,b 2 , а 3 ,…,а n (4)
Согласно шагам ортогонализации система (4) линейно независима, а ее часть b 1 , b 2 –ортогональна.
Предположим, что уже построена линейно независимая система b 1 , b 2 , …, b k-1 , a k ,…, a n , (5)
у которой b 1 , b 2 , …, b k-1 – ортогональны.
На k-том шаге k = 3, n заменим в системе (5) векторa k его ортогональной составляющей относительно системы b 1 , b 2 , …, b k-1 и получим системуb 1 , …,b k , a k+1 , …, a n .
После выполнения n–го шага получим линейно независимую и ортогональную систему векторов b 1 , b 2 , …, b n .
Билет 20 .Дать определение оператора в линейном пространстве. Какой оператор называется линейным.
Оператором называется правило, по которому каждому элементу x X ставится в соответствие единственный элемент y некоторого непустого множества Y . Говорят, что оператор действует из X в Y .
Действие оператора обозначают y = A (x ), y - образ x , x - прообраз y .
Если каждый элемнт y из Y имеет единственный прообраз x из X , y = A (x ), оператор называют взаимно однозначным отображением X в Y или преобразованием X , X - область определения оператора.
Пусть X и Y два линейные пространства. Оператор A , действующий из X в Y , называется линейным оператором , если для любых двух элементовu и v из X и любого числа α справедливо:
A (u + v ) = A (u ) + A (v ) , A (α·u ) = α· A (u ).
Билет 21. Приведите пример линейного оператора. Какие действия над линейными операторами Вы знаете?

Канонические уравнения прямой
Постановка задачи. Найти канонические уравнения прямой, заданной как линия пересечения двух плоскостей (общими уравнениями)
План решения.
Канонические уравнения прямой с направляющим вектором ![]() , проходящей через данную точку
, проходящей через данную точку ![]() , имеют вид
, имеют вид
 . (1)
. (1)
Поэтому, чтобы написать канонические уравнения прямой, необходимо найти ее направляющий вектор и какую-нибудь точку на прямой.
1. Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей, т.е. согласно определению векторного произведения, имеем
 . (2)
. (2)
2. Выбираем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой не параллелен хотя бы одной из координатных плоскостей, то прямая пересекает эту координатную плоскость. Следовательно, в качестве точки на прямой может быть взята точка ее пересечения с этой координатной плоскостью.
3. Подставляем найденные координаты направляющего вектора и точки в канонические уравнения прямой (1).
Замечание. Если векторное произведение (2) равно нулю, то плоскости не пересекаются (параллельны) и записать канонические уравнения прямой не представляется возможным.
Задача 12. Написать канонические уравнения прямой.
Канонические уравнения прямой:
 ,
,
где ![]() – координаты какой-либо точки прямой,
– координаты какой-либо точки прямой, ![]() – ее направляющий вектор.
– ее направляющий вектор.

Найдем какую-либо точку прямой ![]() . Пусть , тогда
. Пусть , тогда

Следовательно, ![]() – координаты точки, принадлежащей прямой.
– координаты точки, принадлежащей прямой.



















