Интегралы от тригонометрических функций. Примеры решений

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).

Содержание

См. также: Метод интегрирования по частям
Таблица неопределенных интегралов
Методы вычисления неопределенных интегралов
Основные элементарные функции и их свойства

Формула интегрирования по частям

При решении примеров этого раздела, используется формула интегрирования по частям:
;
.

Примеры интегралов, содержащих произведение многочлена и sin x, cos x или e x

Вот примеры таких интегралов:
, , .

Для интегрирования подобных интегралов, многочлен обозначают через u , а оставшуюся часть - через v dx . Далее применяют формулу интегрирования по частям.

Ниже дается подробное решение этих примеров.

Примеры решения интегралов

Пример с экспонентой, е в степени х

Определить интеграл:
.

Введем экспоненту под знак дифференциала:
e - x dx = - e - x d(-x) = - d(e - x) .

Интегрируем по частям.

здесь
.
Оставшийся интеграл также интегрируем по частям.
.
.
.
Окончательно имеем:
.

Пример определения интеграла с синусом

Вычислить интеграл:
.

Введем синус под знак дифференциала:

Интегрируем по частям.

здесь u = x 2 , v = cos(2 x+3) , du = ( x 2 )′ dx

Оставшийся интеграл также интегрируем по частям. Для этого вводим косинус под знак дифференциала.


здесь u = x , v = sin(2 x+3) , du = dx

Окончательно имеем:

Пример произведения многочлена и косинуса

Вычислить интеграл:
.

Введем косинус под знак дифференциала:

Интегрируем по частям.

здесь u = x 2 + 3 x + 5 , v = sin 2 x , du = ( x 2 + 3 x + 5)′ dx

Для интегрирования рациональных функций вида R(sin x, cos x) применяют подстановку , которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.

Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида ∫ sin n xdx , ∫ cos n xdx , n>0
a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2. Интегралы вида ∫ tg n xdx , ∫ ctg n xdx , где n – целое.
Необходимо использовать формулы

3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n - нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x . Часто бывает удобным применить приём тригонометрической единицы.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx

Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:

• sin α·cos β = ½(sin(α+β)+sin(α-β))
• cos α·cos β = ½(cos(α+β)+cos(α-β))
• sin α·sin β = ½(cos(α-β)-cos(α+β))

Примеры
1. Вычислить интеграл ∫ cos 4 x·sin 3 xdx .
Делаем замену cos(x)=t . Тогда ∫ cos 4 x·sin 3 xdx =
2. Вычислить интеграл .
Делая замену sin x=t , получаем

3. Найти интеграл .
Делаем замену tg(x)=t . Подставляя, получаем

Интегрирование выражений вида R(sinx, cosx)

Пример №1 . Вычислить интегралы:

Решение.
а) Интегрирование выражений вида R(sinx, cosx) , где R - рациональная функция от sin x и cos x , преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t .
Тогда имеем

Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫ R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:

• Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx , то применяется подстановка cos x = t .
• Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx , то подстановка sin x = t .
• Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx , то подстановка tgx = t или ctg x = t .

В данном случае для нахождения интеграла
применим универсальную тригонометрическую подстановку tg(x/2) = t .
Тогда Ответ:

Интегралы от тригонометрических функций.
Примеры решений

На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника.

Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и .

А сейчас нам потребуются: Таблица интегралов , Таблица производных и Справочник тригонометрических формул . Все методические пособия можно найти на странице Математические формулы и таблицы . Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится.

Но сначала о том, каких интегралов в данной статье нет . Здесь не найдется интегралов вида , – косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений .Также здесь не найдется интегралов с «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.

При нахождении интегралов от тригонометрических функций используется ряд методов:

(4) Используем табличную формулу , единственное отличие, вместо «икса» у нас сложное выражение.

Пример 2

Пример 3

Найти неопределенный интеграл.

Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.

(1) Используем тригонометрическую формулу

(2) Подводим функцию под знак дифференциала.

(3) Используем табличный интеграл .

Пример 4

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Пример 5

Найти неопределенный интеграл.

Степени у нас будут потихоньку повышаться =).
Сначала решение:

(1) Используем формулу

(2) Используем основное тригонометрическое тождество , из которого следует, что .

(3) Почленно делим числитель на знаменатель.

(4) Используем свойство линейности неопределенного интеграла.

(5) Интегрируем с помощью таблицы.

Пример 6

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Также существуют интегралы от тангенсов и котангенсов, которые находятся в более высоких степенях. Интеграл от тангенса в кубе рассмотрен на уроке Как вычислить площадь плоской фигуры? Интегралы от тангенса (котангенса) в четвертой и пятой степенях можно раздобыть на странице Сложные интегралы .

Понижение степени подынтегральной функции

Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы , и , причем последняя формула чаще используется в обратном направлении: .

Пример 7

Найти неопределенный интеграл.

Решение:

В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу (понизив степень подынтегральной функции). Обратите внимание, что я сократил решение. По мере накопления опыта интеграл от можно находить устно, это экономит время и вполне допустимо при чистовом оформлении заданий. В данном случае целесообразно не расписывать и правило , сначала устно берем интеграл от 1, затем – от .

Пример 8

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Таки обещанное повышение степени:

Пример 9

Найти неопределенный интеграл.

Сначала решение, потом комментарии:

(1) Готовим подынтегральную функцию для применения формулы .

(2) Собственно применяем формулу.

(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но, на мой взгляд, так удобнее.

(4) Используем формулу

(5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы .

(6) Приводим подобные слагаемые (здесь я почленно разделил и выполнил сложение ).

(7) Собственно берём интеграл, правило линейности и метод подведения функции под знак дифференциала выполняем устно.

(8) Причесываем ответ.

! В неопределенном интеграле нередко ответ можно записать несколькими способами

В только что рассмотренном примере окончательный ответ можно было записать иначе – раскрыть скобки и даже это сделать еще до интегрирования выражения, то есть вполне допустима следующая концовка примера:

Вполне возможно, что такой вариант даже удобнее, просто я объяснил так, как сам привык решать). Вот еще один характерный пример для самостоятельного решения:

Пример 10

Найти неопределенный интеграл.

Это пример решается двумя способами, и у Вас могут получиться два совершенно разных ответа (точнее говоря, они будут выглядеть совершенно по-разному, а с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.

Подытоживая параграф, сделаем вывод: любой интеграл вида , где и – чётные числа, решается методом понижения степени подынтегральной функции.
На практике мне встречались интегралы с 8 и 10 степенями, решать их ужасный гемор приходилось, понижая степень несколько раз, в результате чего получались длинные-длинные ответы.

Метод замены переменной

Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле , основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция и её производная :
(функции , не обязательно находятся в произведении)

Пример 11

Найти неопределенный интеграл.

Смотрим в таблицу производных и замечаем формулы , , то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же обозначать за – синус или косинус?! Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится.

Общий ориентир: в похожих случаях за нужно обозначить функцию, которая находится в знаменателе.

Прерываем решение и проводим замену

В знаменателе у нас всё хорошо, всё зависит только от , теперь осталось выяснить, во что превратится .
Для этого находим дифференциал :

Или, если короче:
Из полученного равенства по правилу пропорции выражаем нужное нам выражение:

Итак:

Теперь всё подынтегральное выражение у нас зависит только от и можно продолжать решение

Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.

Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле .

А сейчас два примера для самостоятельного решения:

Пример 12

Найти неопределенный интеграл.

Пример 13

Найти неопределенный интеграл.

Полные решения и ответы в конце урока.

Пример 14

Найти неопределенный интеграл.

Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что же обозначать за , синус или косинус?

Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за другую функцию, но есть:

Общий ориентир: за нужно обозначить ту функцию, которая, образно говоря, находится в «неудобном положении» .

Мы видим, что в данном примере студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе.

Поэтому проведем замену:

Если у кого остались трудности с алгоритмом замены переменной и нахождением дифференциала , то следует вернуться к уроку Метод замены переменной в неопределенном интеграле .

Пример 15

Найти неопределенный интеграл.

Анализируем подынтегральную функцию, что нужно обозначить за ?
Вспоминаем наши ориентиры:
1) Функция, скорее всего, находится в знаменателе;
2) Функция находится в «неудобном положении».

Кстати, эти ориентиры справедливы не только для тригонометрических функций.

Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена . В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с ? Во-первых, «отщипываем» один косинус:

Мы резервируем под наш «будущий» дифференциал

А выражаем через синус с помощью основного тригонометрического тождества:

Вот теперь замена:

Общее правило: Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за – обозначить другую функцию. Речь идет только об интегралах, где есть косинусы и синусы.

В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за обозначили синус.

Пример 16

Найти неопределенный интеграл.

Степени идут на взлёт =).
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: , , , и т.д.

Пример 17

Найти неопределенный интеграл.

Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену: . Я использую не букву , а букву , это не является каким-то правилом, просто опять же я так привык решать.

Здесь удобнее находить дифференциал , для этого из равенства , я выражаю :
Навешиваю на обе части арктангенс:

Арктангенс и тангенс взаимно уничтожаются:

Таким образом:

На практике можно не расписывать так подробно, а просто пользоваться готовым результатом:

! Выражение справедливо только в том случае, если под синусами и косинусами у нас просто «иксы», для интеграла (о котором мы еще поговорим) всё будет несколько иначе!

При замене синусы и косинусы у нас превращаются в следующие дроби:
, , эти равенства основаны на известных тригонометрических формулах: ,

Итак, чистовое оформление может быть таким:

Проведем универсальную тригонометрическую подстановку:

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму

Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида

Воспользовавшись известными тригонометрическими формулами

(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам

(5)

(6)

Пример 1. Найти

Решение. По формуле (2) при

Пример 2. Найти интеграл от тригонометрической функции

Решение. По формуле (3) при

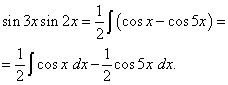
Пример 3. Найти интеграл от тригонометрической функции

Решение. По формуле (4) при получаем следующее преобразование подынтегрального выражения:

Применяя формулу (6), получим

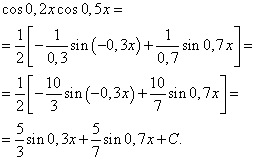
Интеграл произведения степеней синуса и косинуса одного и того же аргумента

Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

(7)

В частных случаях один из показателей (m или n ) может равняться нулю.

При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен - sin x dx ) .

Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.

Пусть имеет место первый случай, а именно показатель n = 2k + 1 - нечётный. Тогда, учитывая, что

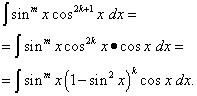
Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t . Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx , выражая остальную часть подынтегральной функции через cos x и полагая t = cos x . Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса , когда хотя бы один из показателей - нечётный . Всё дело в том, что частное степеней синуса и косинуса - это частный случай их произведения : когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень - отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени - только чётные. О них - следующем абзаце.

Если же оба показателя m и n – чётные, то, используя тригонометрические формулы

понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей - отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится . Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.

Пример 4. Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса – нечётный. Поэтому представим

t = sin x (тогда dt = cos x dx ). Тогда получим

Возвращаясь к старой переменной, окончательно найдём

Пример 5. Найти интеграл от тригонометрической функции

.

Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим

и произведём замену переменной t = sin x (тогда dt = cos x dx ). Тогда получим

Раскроем скобки

и получим

Возвращаясь к старой переменной, получаем решение

Пример 6. Найти интеграл от тригонометрической функции

Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:

Тогда получим

Во втором интеграле произведём замену переменной, полагая t = sin2x . Тогда (1/2)dt = cos2x dx . Следовательно,

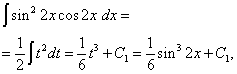
Окончательно получаем

Использование метода замены переменой

Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус - в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t , но и tgx = t и ctgx = t .

Пример 8. Найти интеграл от тригонометрической функции

.

Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:

.

Пример 9. Найти интеграл от тригонометрической функции

Решение. Преобразуем тангенс в отношение синуса и косинуса:

Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:

.

Возвращаясь к первоначальной переменной, окончательно получаем:

.

Пример 10. Найти интеграл от тригонометрической функции

Решение. Произведём замену переменной: , тогда .

Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество :

Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt ). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:

Возвращаясь к первоначальной переменной, окончательно получаем:

.

Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение

Универсальная тригонометрическая подстановка

Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:

Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.

Пример 12. Найти интеграл от тригонометрической функции

.

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой . Тогда
.

Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда

Таблица первообразных ("интегралов"). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.

Таблица первообразных ("интегралов"). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром).
Интеграл степенной функции.	Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
	Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.	Интеграл экспоненциальной функции.
Интеграл, равняющийся натуральному логорифму.	Интеграл: "Длинный логарифм".
	Интеграл: "Длинный логарифм".
Интеграл: "Высокий логарифм".	Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму.
Интеграл: "Высокий логарифм".
Интеграл косинуса.	Интеграл синуса.
Интеграл, равный тангенсу.	Интеграл, равный котангенсу.
Интеграл, равный как арксинусу, так и арккосинусу
Интеграл, равный как арксинусу, так и арккосинусу.	Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл равный косекансу.	Интеграл, равный секансу.
Интеграл, равный арксекансу.	Интеграл, равный арккосекансу.
Интеграл, равный арксекансу.	Интеграл, равный арксекансу.
Интеграл, равный гиперболическому синусу.	Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому синусу, где sinhx - гиперболический синус в ангийской версии.	Интеграл, равный гиперболическому косинусу, где sinhx - гиперболический синус в ангийской версии.
Интеграл, равный гиперболическому тангенсу.	Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому секансу.	Интеграл, равный гиперболическому косекансу.

Формулы интегрирования по частям. Правила интегрирования.

Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования.
Интегрирование произведения (функции) на постоянную:
Интегрирование суммы функций:
неопределенные интегралы:
Формула интегрирования по частям определенные интегралы:
Формула Ньютона-Лейбница определенные интегралы:	Где F(a),F(b)-значения первообразных в точках b и a соответственно.

Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.

Если x - независимая переменная, то:

Таблица производных. Табличные производные."таблица производный"-да, к сожалению, именно так их и ищут в интернете
	Производная степенной функции
	Производная экспоненты
Производная сложной экспоненциальной функции	Производная экспоненциальной функции
Производная логарифмической функции	Производная натурального логарифма
	Производная натурального логарифма функции
Производная синуса	Производная косинуса
Производная косеканса	Производная секанса
Производная арксинуса	Производная арккосинуса
Производная арксинуса	Производная арккосинуса
Производная тангенса	Производная котангенса
Производная арктангенса	Производная арккотангенса
Производная арктангенса	Производная арккотангенса
Производная арксеканса	Производная арккосеканса
Производная арксеканса	Производная арккосеканса
Производная гиперболического синуса Производная гиперболического синуса в английской версии	Производная гиперболического косинуса Производная гиперболического косинуса в английской версии
Производная гиперболического тангенса	Производная гиперболического котангенса
Производная гиперболического секанса	Производная гиперболического косеканса

Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции.
Производная произведения (функции) на постоянную:
Производная суммы (функций):
Производная произведения (функций):
Производная частного (функций):
Производная сложной функции:

Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).

Основное логарифмическое тождество
Покажем как можно любую функцию вида a b сделать экспоненциальной. Поскольку функция вида е х называется экспоненциальной, то
Любая функция вида a b может быть представлена в виде степени десяти

Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045…) ln(e)=1; ln(1)=0

Ряд Тейлора. Разложение функции в ряд Тейлора.

Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:

При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.

Ряд Тейлора в окрестности точки a имеет виды:

1) , где f(x) - функция, имеющая при х=а производные всех порядков. R n - остаточный член в ряде Тейлора определяется выражением

2)

k-тый коэффициент (при х k) ряда определяется формулой

3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)

при a=0

члены ряда определяются по формуле

Условия применения рядов Тейлора.

1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).

2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.

Свойства рядов Тейлора.

Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.

Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

Ряды Тейлора применяются при аппроксимации (приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis - линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.

Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.

Примеры некоторых распространенных разложений степенных функций в ряды Маклорена(=Макларена, Тейлора в окрестностях точки 0)

Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1